Rekurencja (rekursja)

Co to jest Rekurencja?

Zacznijmy od żartu. Rekurencja (ang.recursion) występuje, gdy definicja typu czy funkcji odwołuje się sama do siebie. Przykładem rekurencyjnej definicji funkcji może być definicja ciągu Fibonacciego: $$ F_n = \begin{cases} 1,& \text{if } x = 0\newline 1,& \text{if } x = 1\newline F_{n-1} + F_{n-2},& \text{if } x \geq 2 \newline \end{cases} $$ A przykładem rekurencyjnej definicji struktury danych (typu) może być definicja listy jednokierunkowej:

struct node
{
  int data;           // some integer data
  struct node *next;  // pointer to another struct node
};

Dzięki rekurencji łatwo można w prosty sposób zdefiniować niektóre zbiory fraktalne, np. trójkąt Sierpińskiego:

Wieże Hanoi

Mamy trzy stosy. Na jednym w nich od najmniejszego do największego (patrząc z góry) ułożone jest $N$ krążków. Pozostałe 2 stosy są puste. Zadanie polega na przeniesieniu krążków na wybrany z dwóch pozostałych stosów tak żeby zachować kolejność. Zasady:

• jednocześnie przenosić można tylko jeden krążek,
• większy krążek nigdy nie może leżeć na mniejszym.

Można zajrzeć tutaj po dokładniejszy opis.

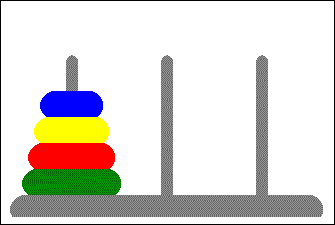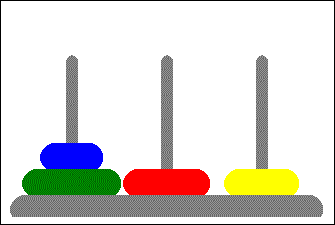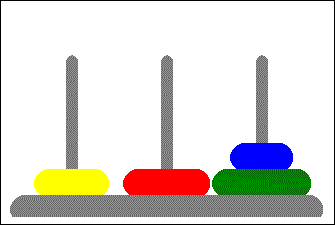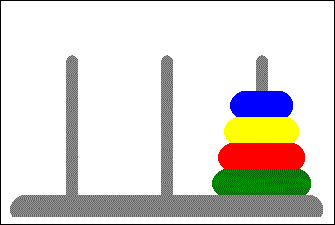
Wyzwanie 1.

Spróbuj na kartce papieru rozwiązać zagadkę dla 3 krążków.

Pseudokod rozwiązania rekurencyjnego

function move(n, source, target, buffer):
    if n == 0:
       return

    # move n - 1 disks from source to helping tower, so they are out of the way
    move(n - 1, source, buffer, target)

    # move the nth disk from source to target
    target.append(source.pop())

    # move the n - 1 disks that we left on helping onto target
    move(n - 1, buffer, target, source)

Co należy zrobić?

1. Zaimplementuj rekurencyjną funkcję wiezeHanoi(N:int), która rozwiąże problem i jednocześnie na konsoli wyświetli jakąś wizualizację wykonanych ruchów. (Podpowiedź: Krążki reprezentuj przez liczby naturalne a stosy przez listy.)
2. Czy potrafisz wyjaśnić dlaczego zaprezentowany algortym działa?
3. Jak zależy ilość przestawień od liczby krążków?