Sortowanie szybkie

Na czym polega sortowanie szybkie?

Algorytm sortowania szybkiego (ang. quick sort), podobnie jak sortowanie przez scalanie, wykorzystuje metodę ,,dziel i zwyciężaj’’ (ang. divide-and-conquer).

Ogólny opis algorytmu quicksort jest następujący:

• Wybierz element tablicy zwany z angielskiego pivot.
• Podziel tablicę na dwie części - zawierającym elementy większe i elementy mniejsze od pivota. Po tym kroku tablica sortowana powinna wyglądać następująco: [elementy<pivot, pivot, elementy>pivot].
• Zastosuj tę strategię rekurencyjnie dla obydwu części.

Rekursja kończy się gdy ciąg do posortowania ma długość równą 1 - ciąg o długości 1 zawsze jest posortowany.

Kluczowym elementem algorytmu jest procedura partycjonowania (ang. partitioning). Istnieje kilka różnych strategii wykonywania podziału. Drugin ważnym elementem sortowania szybkiego jest metoda wyboru pivota. Typowo wykorzystuje się element ostatni, ale schemat jego wyboru jest dowolny. Optymalny pivot to taki który dzieli nam tablicę na dwie równe części.

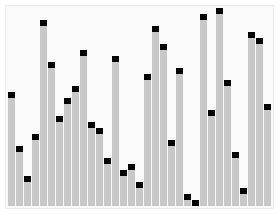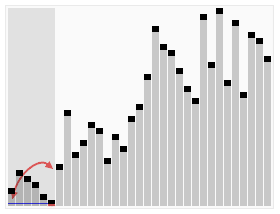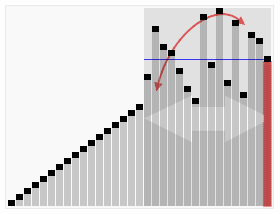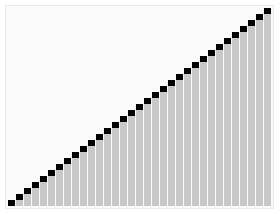
(Grafika pochodzi z artykułu w angielskojęzycznej Wikipedii)

Wizualizacja

Pseudokod

algorithm quick_sort(A, lo, hi) is
    if lo < hi then
        p := partition(A, lo, hi)
        quicksort(A, lo, p)
        quicksort(A, p + 1, hi)

algorithm partition(A, lo, hi) is
    """
    Hoare partitioning method (1959)
    """
    pivot := A[lo + (hi - lo) / 2]
    i := lo - 1
    j := hi + 1
    loop forever
        do
            i := i + 1
        while A[i] < pivot
        do
            j := j - 1
        while A[j] > pivot
        if i >= j then
            return j
        swap A[i] with A[j]

Aby posortować tablicę A należy wywołać zaimplementowaną funckję następująco: quick_sort(A, 0, len(A)-1).

Co należy zaimplementować?

1. Zaimplementuj funkcję quick_sort(), która jako argument przyjmuje listę a zwraca listę posortowaną.
2. Porównaj czas sortowania list o długości 5, 10, 50, 100, 1000 elementów przy pomocy algorytmów quick_sort() i merge_sort().

Pytania

1. Jak rośnie czas wykonania algorymtu wraz ze wzrostem długości danych N (liniowo, kwadratowo, logarytmicznie, …)?
2. Jaka jest największa słabość algorytmu sortowania szybkiego?
3. Jakie znasz metody wyboru pivota? Która jest najlepsza?
4. Czym jest zrandomizowany quicksort?
5. Czy algorytm sortowania szybkiego jest zawsze szybszy od algorytmu sortowania przez scalanie? Dlaczego?