Sortowanie przez scalanie

Na czym polega sortowanie przez scalanie?

Algorytm sortowania przez scalanie (ang. merge sort) wykorzystuje metodę ,,dziel i zwyciężaj’’ (ang. divide-and-conquer). Algorytmy tego typu wywołują same siebie (jeden lub więcej razy), tzn. mają strukturę rekurencyjną. Metoda ,,dziel i zwyciężaj’’ polega na podzieleniu problemu na mniejsze podproblemy, rozwiązaniu ich a następnie połączeniu rozwiązań podproblemów w celu uzyskania rozwiązania początkowego, pełnego problemu.

Ogólny opis algorytmu sortowania przez scalanie jest następujący:

• Podziel $n$-elementowy ciąg na dwa podciągi po $n/2$ elementów każdy.
• Posortuj otrzymane podciągi, używając rekurencyjnie sortowania przez scalanie.
• Połącz posortowanie podciągi w jeden posortowany ciąg.

Rekursja kończy się gdy ciąg do posortowania ma długość równą 1 - ciąg o długości 1 zawsze jest posortowany.

Kluczowym elementem algorytmu jest procedura $\text{MERGE}(A,p,q,r)$, gdzie $A$ to tablica, a $p,~q,~r$ są indeksami ($p\le q\le r$). Procedura zakłada, że podciągi $A[p..q]$ i $A[q..r]$ są posortowane. Po jej wywołaniu tablica $A[p..r]$ jest posortowana. (Opracowano na podstawie książki T. H. Cormen i in. ,,Wprowadzenie do algorytmów’’.)

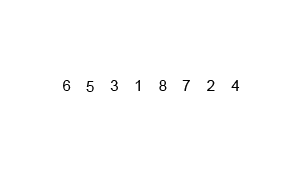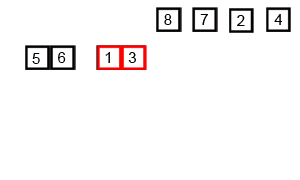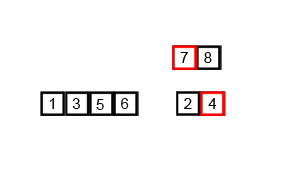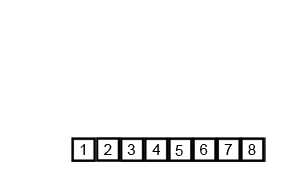
Wizualizacja

Pseudokod

procedure mergeSort( A, p, r)
  // posortuj tablicę A -> mergeSort(A, 0, length(A)-1)
  if p < r
    q = floor((p+r)/2)
    mergeSort(A, p, q)
    mergeSort(A, q+1, r)
    merge(A, p, q, r)
  endif

procedure merge(A, p, q, r)
  n1 = q - p + 1
  n2 = r - q
  L[0..n1] i R[0..n2] to puste tablice
  for i = 0 to n1
    L[i] = A[p+i]
  for i = 0 to n2
    R[j] = A[q+j+1]
  L[n1] = infinity
  L[n2] = infinity
  i = 0
  j = 0
  for k = p to r
    if L[i] <= R[j]
      A[k] = L[i]
      i++
    else
      A[k] = R[j]
      j++
    endif

Co należy zaimplementować?

1. Zaimplementuj funkcję merge_sort(), która jako argument przyjmuje listę a zwraca listę posortowaną.
2. Porównaj czas sortowania list o długości 5, 10, 50, 100, 1000 elementów przy pomocy algorytmów mergeSort() i insertionSort().

Pytania

1. Jak rośnie czas wykonania algorymtu wraz ze wzrostem długości danych N (liniowo, kwadratowo, logarytmicznie, …)?
2. Czy algorytm sortowania przez scalanie jest zawsze szybszy od algorytmu sortowania przez wstawianie?
3. Jak zbudować hybrydę algorytmów sortowania przez scalanie i sortowania przez wstawianie, która będzie szybsza od sortowania przez scalanie?